Answer:
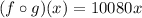 , where x is the number of weeks.
, where x is the number of weeks.
It computes the number of minutes in x weeks.
Step-by-step explanation:
Given : The function defined by
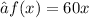 computes the number of minutes in x hours, and the function defined by
computes the number of minutes in x hours, and the function defined by
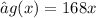 , computes the number of hours in x weeks.
, computes the number of hours in x weeks.
Then , the composite function is given by :-
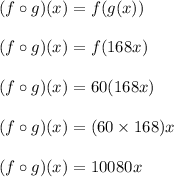
Hence, the required composite function is :
 , where x is the number of weeks.
, where x is the number of weeks.
Simply, the above composite function computes the number of minutes in x weeks.