Question

Suppose you toss a fair coin 10 times, let X denote the number of heads. (a) What is the probability that X=5? (b) What is the probability that X greater or equal than 5? (c) If I want to make sure that the P(X ≤ a) > 0.8, what is the minimum value of a? (a is an integer

Answer 1

Answer: The required answers are

(a) 0.25, (b) 0.62, (c) 6.

Step-by-step explanation: Given that we toss a fair coin 10 times and X denote the number of heads.

We are to find

(a) the probability that X=5

(b) the probability that X greater or equal than 5

(c) the minimum value of a such that P(X ≤ a) > 0.8.

We know that the probability of getting r heads out of n tosses in a toss of coin is given by the formula of binomial distribution as follows :

`P(X=r)=^nC_r\left((1)/(2)\right)^r\left((1)/(2)\right)^(n-r).`

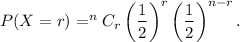
(a) The probability of getting 5 heads is given by

`P(X=5)\\\\\\=^(10)C_5\left((1)/(2)\right)^5\left((1)/(2)\right)^(10-5)\\\\\\=(10!)/(5!(10-5)!)(1)/(2^(10))\\\\\\=0.24609\\\\\sim0.25.`

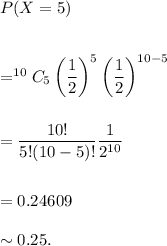
(b) The probability of getting 5 or more than 5 heads is

`P(X\geq 5)\\\\=P(X=5)+P(X=6)+P(X=7)+P(X=8)+P(X=9)+P(X=10)\\\\=^(10)C_5\left((1)/(2)\right)^5\left((1)/(2)\right)^(10-5)+^(10)C_6\left((1)/(2)\right)^6\left((1)/(2)\right)^(10-6)+^(10)C_7\left((1)/(2)\right)^7\left((1)/(2)\right)^(10-7)+^(10)C_8\left((1)/(2)\right)^8\left((1)/(2)\right)^(10-8)+^(10)C_9\left((1)/(2)\right)^9\left((1)/(2)\right)^(10-9)+^(10)C_(10)\left((1)/(2)\right)^(10)\left((1)/(2)\right)^(10-10)\\\\\\=0.24609+0.20507+0.11718+0.04394+0.0097+0.00097\\\\=0.62295\\\\\sim 0.62.`

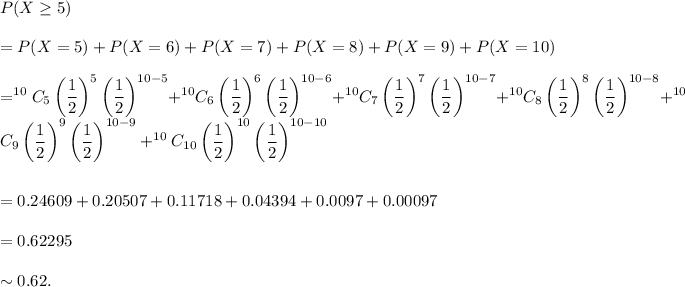
(c) Proceeding as in parts (a) and (b), we see that

if a = 10, then

`P(X\leq 0)=0.00097,\\\\P(X\leq 1)=0.01067,\\\\P(X\leq 2)=0.05461,\\\\P(X\leq 3)=0.17179,\\\\P(X\leq 4)=0.37686,\\\\P(X\leq 5)=0.62295,\\\\P(X\leq 6)=0.82802.`

Therefore, the minimum value of a is 6.

Hence, all the questions are answered.