Answer:
20.44 Hz
Step-by-step explanation:
We are given that
Length of strand=L=11 m
Mass of strand=m=6 g=
 (1kg=1000g)
(1kg=1000g)
Mass of hanging object=M=6 kg
Distance of pulley from the wall=d=8 m
We have to find the fundamental frequency of(Hz) of its vibration.
Velocity=
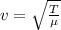
Where T= Tension force


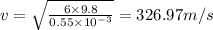
Frequency=
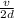
Substitute the values in the formula
Then, we get
Frequency=
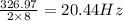
Hence, the fundamental frequency of ist vibration=20.44 Hz