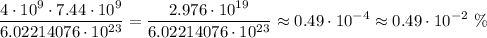Question

If you started counting when you first learned how to count and then counted by ones, eight hours a day, 5 days a week for 50 weeks a year, you would be judged a 'good counter' if you could reach 4 billion by the time you retired at age 65. If every human on Earth (7.44×10⁹) were to count this way until retirement, what percentage of a mole would they count?

Answer 1

The number they would count is
`\approx 0.49\cdot10^(-2)\ \%}`

Explanation:

One mole is equal to 6.02214076x10^23 particles. In order to know the number counted by every human on Earth we simply multiply the number of humans times the count a "good counter" can achieve, 4x10^9x7.44x10^9 (for USA, change to 4x10^12 if you use de British English definition). Thus:

`\displaystyle{(4\cdot10^9\cdot7.44\cdot10^9)/(6.02214076\cdot10^(23))=(2.976\cdot 10^(19))/(6.02214076\cdot10^(23))\approx 0.49 \cdot 10^(-4)\approx 0.49\cdot10^(-2)\ \%}`