Question

The LB Company has long manufactured a light bulb with an average life of 5400 hours. Company researchers have recently developed a new filament which they believe will extend bulb life. To test this claim, the company hires a statistician, who takes a random sample of 95 bulbs and measures the amount of time until each bulb burned out. The mean lifetime of the sample of bulbs is 5483 hours. (We may assume as known that the population is normally distributed with a standard deviation of 500 hours.) Can we conclude at a 6% level of significance that the new filament yields a longer bulb life?

Answer 1

Answer with explanation:

Let
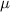`\mu` be the average life of light bulbs.

As per given , we have

Null hypothesis :
`H_0 : \mu =5400`

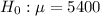
Alternative hypothesis :
`H_a : \mu >5400`

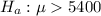
Since
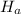`H_a` is right-tailed and population standard deviation is also known, so we perform right-tailed z-test.

Formula for Test statistic :
`z=\frac{\overlien{x}-\mu}{(\sigma)/(√(n))}`

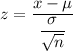
where, n= sample size

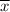`\overline{x}`= sample mean

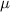`\mu`= Population mean

`\sigma`=population standard deviation

For
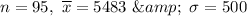`n=95,\ \overline{x}=5483\ \&\ \sigma=500`, we have

`z=(5483-5400)/((500)/(√(95)))=1.61796786124\approx1.6180`

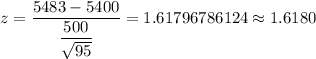
Using z-value table , Critical one-tailed test value for 0.06 significance level :

`z_(0.06)=1.5548`

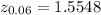
Decision : Since critical z value (1.5548) < test statistic (1.6180), so we reject the null hypothesis .

[We reject the null hypothesis when critical value is less than the test statistic value .]

Conclusion : We have enough evidence at 0.06 significance level to support the claim that the new filament yields a longer bulb life