Answer:
183.710 feet
Explanation:
The angle of elevation from the first point to the top of the building is 45° i.e.∠ABD = 45°
The angle of elevation from the second point to the top of the building is 60° i.e.∠ACD = 60°
The distance from the second point to the top of the building is 150 ft i.e.AC = 150 feet
We are supposed to find the distance from the first observation point to the top of the tower i.e.AB = x
In ΔACD
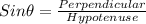
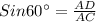
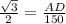
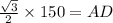
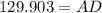
In ΔABD
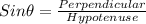
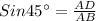
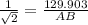
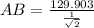
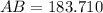
Hence the distance from the first observation point to the top of the tower is 183.710 feet