Question

A graph shows the number of texts, numbered 10 to 100, on the x-axis, and the total cost in dollars, numbered 3 to 27, on the y-axis. A straight red line with a positive slope, labeled Emilia, begins at (0, 10), and a straight blue line with a positive slope, labeled Hiroto, begins at (0, 20). Both lines intersect at point (50, 22.5).

Hiroto’s texting plan costs $20 per month, plus $0.05 per text message that is sent or received. Emilia’s plan costs $10 per month and $0.25 per text. Using the graph below, which statement is true?

Hiroto’s plan costs more than Emilia’s plan when more than 50 texts are sent.
Both plans cost the same when 22 texts are sent.
Emilia’s plan costs more than Hiroto’s plan when more than 22 texts are sent.
Both plans cost the same when 50 texts are sent.

Answer 1

Both plans cost the same when 50 texts are sent

Explanation:

Answer 2

Both plans cost the same when 50 texts are sent

Explanation:

Let

x ---->the number of texts

y ----> the total cost in dollars

we know that

The linear equation in slope intercept form is equal to

`y=mx+b`

where

m is the slope or unit rate

b is the y-intercept or initial value

we have that

Emilia’s plan (Red line)

The slope is

`m=\$0.25\ per\ text`

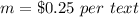
The y-intercept is

`b=\$10`

substitute

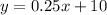`y=0.25x+10` ----> equation A

Hiroto’s plan (Blue line)

The slope is

`m=\$0.05\ per\ text`

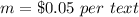
The y-intercept is

`b=\$20`

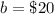
substitute

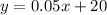`y=0.05x+20` ----> equation B

The solution of the system of equations A and B is the point of intersection both graphs

The intersection point is given

The intersection point is (50,22.5)

That means----> For x=50 texts, the cost is equal in both plans

Verify each statement

case a) Hiroto’s plan costs more than Emilia’s plan when more than 50 texts are sent

The statement is false

Because

Emilia’s plan costs more than Hiroto’s plan when more than 50 texts are sent

Verify

For x=100 texts ----> 100 > 50

Emilia's plans

`y=0.25(100)+10=\$35`

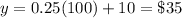
Hiroto's plans

`y=0.05(100)+20=\$25`

`\$35> \$25`

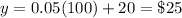
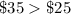
case b) Both plans cost the same when 22 texts are sent

The statement is false

Because

Both plans cost the same when 50 texts are sent

case c) Emilia’s plan costs more than Hiroto’s plan when more than 22 texts are sent.

The statement is false

Because

Emilia’s plan costs more than Hiroto’s plan when more than 50 texts are sent

case d) Both plans cost the same when 50 texts are sent

The statement is true