Question

A 0.060 ???????? tennis ball, moving with a speed of 5.28 m/???? , has a head-on collision with a 0.080 ???????? ball initially moving in the same direction at a speed of 3.00 m/ ???? . Assume that the collision is perfectly elastic. Determine the velocity (speed and direction) of both the balls after the collision.

Answer 1

Step-by-step explanation:

It is given that,

Mass of the tennis ball,
`m_1=0.06\ kg`

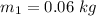
Initial speed of tennis ball,
`u_1=5.28\ m/s`

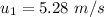
Mass of ball,
`m_2=0.08\ kg`

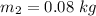
Initial speed of ball,
`u_2=3\ m/s`

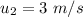
In case of elastic collision, the momentum remains conserved. The momentum equation is given by :

`m_1u_1+m_2u_2=m_1v_1+m_2v_2`

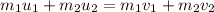
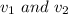`v_1\ and\ v_2` are final speed of tennis ball and the ball respectively.

`0.06* 5.28+0.08* 3=0.06v_1+0.08v_2`

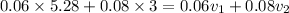
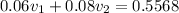`0.06v_1+0.08v_2=0.5568`..............(1)

We know that the coefficient of restitution is equal to 1. It is given by :

`(v_2-v_1)/(u_1-u_2)=1`

`(v_2-v_1)/(5.28-3)=1`

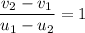
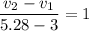
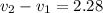`{v_2-v_1}=2.28`.................(2)

On solving equation (1) and (2) to find the values of velocities after collision.

`v_1=5.28\ m/s`

`v_2=3\ m/s`

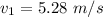
So, the speed of both balls are 5.28 m/s and 3 m/s respectively. Hence, this is the required solution.