Answer:
Answered
Step-by-step explanation:
Given
Heat source temperature T_1= 1200° C = 1473 K
thermal efficiency η =40% = 0.4
maximum work output W_{max} = 490 kJ
we know that
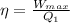
Heat supplied Q_1 can be calculated as 1225 kJ by putting values of η and W_{max} in the above equation.
Now we also know that

where Q_2 is the heat rejected to the sink
now
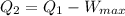
therefore, Q_2= 1225-490= 735 kJ
to calculate sink temperature T_2
we use the formula

putting values of η and T_1 we get
T_2= 883.8 K= 610.8° C