Answer:
4096 is the simplified form of
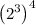
Option: B
Explanation:
Given that
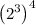
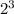 represents 2 to the power 3 that means the number appears three times in multiplying.
represents 2 to the power 3 that means the number appears three times in multiplying.


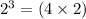

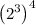 represents 2³ to the power 4 means the number 4 appears four times in multiplying.
represents 2³ to the power 4 means the number 4 appears four times in multiplying.
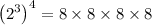
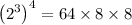
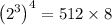
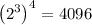
Hence the simplified form of
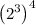 is 4096.
is 4096.