Question

If we sample from a small finite population without​ replacement, the binomial distribution should not be used because the events are not independent. If sampling is done without replacement and the outcomes belong to one of two​ types, we can use the hypergeometric distribution. If a population has A objects of one​ type, while the remaining B objects are of the other​ type, and if n objects are sampled without​ replacement, then the probability of getting x objects of type A and nminusx objects of type B under the hypergeometric distribution is given by the following formula. In a lottery​ game, a bettor selects six numbers from 1 to 56 ​(without repetition), and a winning six​-number combination is later randomly selected. Find the probabilities of getting exactly four winning numbers with one ticket.​ (Hint: Use Aequals6​, Bequals50​, nequals6​, and xequals4​.)

Answer 1

5/4324 = 0.001156337

Explanation:

To better understand the hyper-geometric distribution consider the following example:

There are 100 senators in the US Congress, and suppose 60 of them are republicans so 100 - 60 = 40 are democrats).

We extract a random sample of 30 senators and we want to answer this question:

What is the probability that 10 senators in the sample are republicans (and of course, 30 - 10 = 20 democrats)?

The answer using the h-g distribution is:

`\large \frac{\binom{60}{10}\binom{100-60}{30-10}}{\binom{100}{30}}=\frac{\binom{60}{10}\binom{40}{20}}{\binom{100}{30}}`

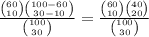
Now, imagine there are 56 senators (56 lottery numbers), 6 are republicans (6 winning numbers and 50 losers), we extract a sample of 6 senators (the bettor selects 6 numbers). What is the probability that 4 senators are republicans? (What is the probability that 4 numbers are winners?).

As we see, the situation is exactly the same, but changing the numbers. So the answer would be

`\large \frac{\binom{6}{4}\binom{56-6}{6-4}}{\binom{56}{6}}=\frac{\binom{6}{4}\binom{50}{2}}{\binom{56}{6}}`

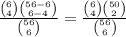
Now compute each combination separately:

`\large \binom{6}{4}=(6!)/(4!2!)=15\\\\\binom{50}{2}=(50!)/(2!48!)=1225\\\\\binom{50}{6}=(50!)/(6!44!)=15890700`

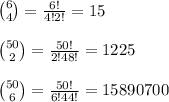
and now replace the values:

`\large \frac{\binom{6}{4}\binom{50}{2}}{\binom{56}{6}}=(15*1225)/(15890700)=(18375)/(15890700)=(5)/(4324)`

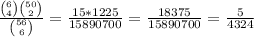
and that is it.

If the decimal expression is preferred then divide the fractions to get 0.001156337