Answer:
Velocity of the players afterwards = 2.88 m/s towards east.
Step-by-step explanation:
Mass of football player A
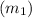 = 91.5 kg
= 91.5 kg
Velocity of player A
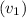 = 2.73 m/s
= 2.73 m/s
Mass of football player B
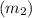 =63.5 kg
=63.5 kg
Velocity of player B
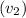 = 3.09 m/s
= 3.09 m/s
Since both players move in same direction east, so their velocity afterwards will also be in same direction east.
By law of conservation of momentum we have:
Momentum before collision = Momentum after collision
This can be written as:
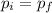
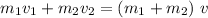
where
 is the velocity of the players together afterwards.
is the velocity of the players together afterwards.
We can plugin the given value to find

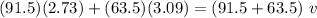
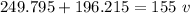
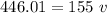
Dividing both sides by 155.
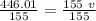
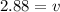
∴
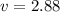 m/s
m/s
Velocity of the players afterwards = 2.88 m/s towards east.