Question

In reading the instruction manual that came with your garagedoor opener, you see that the transmitter unit in your car produces a 250 mW, 350 MHz signal and that the receiver unit is supposed to respond to a radio wave at this frequency if the electric field amplitude exceeds 0.10 V/m. You wonder if this is really true. To find out, you put fresh batteries in the transmitter and start walking away from your garage while opening and closing the door. Your garage door finally fails to respond when you’re 42 m away What is the electric field amplitude at the receiver when it first fails?

Answer 1

0.09221 V/m

Step-by-step explanation:

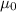`\mu_0` = Vacuum permeability =
`4\pi * 10^(-7)\ H/m`

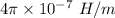
P = Power of transmitter = 250 mW

r = Distance to source = 42 m

c = Speed of light =
`3* 10^8\ m/s`

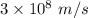
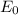`E_0` = Electric field amplitude

Intensity of a wave is given by

`I=(P)/(4\pi r^2)\\\Rightarrow I=(250* 10^(-3))/(4\pi * 42^2)\\\Rightarrow I=1.12779* 10^(-5)\ W/m^2`

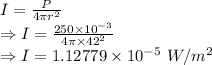
Intensity is also given by

`I=(E_0^2)/(2\mu_0 c)\\\Rightarrow E_0=√(I2\mu_0 c)\\\Rightarrow E_0=\sqrt{1.12779* 10^(-5)* 2* 4\pi * 10^(-7)* 3* 10^8}\\\Rightarrow E_0=0.09221\ V/m`

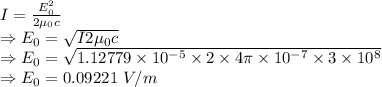
The electric field amplitude at the receiver when it first fails is 0.09221 V/m