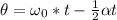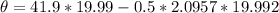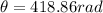1 Answer

Cpg · Answer 1 · 2020-10-20T04:36:44+0000

To solve this problem it is necessary to apply the concepts of displacement, speed and acceleration given by classical mechanics.

Our previously given values correspond to,

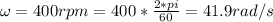
$\omega =400rpm = 400*(2*pi)/(60)= 41.9 rad/s$

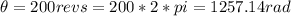
$\theta=200 revs = 200*2*pi= 1257.14 rad$

By definition we know that angular displacement is defined by,

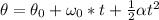
$\theta = \theta_0 +\omega_0*t+(1)/(2)\alpha t^2$

Here we know that there is no initial deployment so replacing the values we have to,

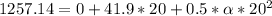
$1257.14 = 0+41.9*20+0.5*\alpha*20^2$

Solving for
$\alpha$

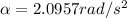
$\alpha = 2.0957 rad/s^2$

From the acceleration description equations we know that,

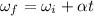
$\omega_f = \omega_i+\alpha t$

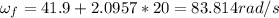
$\omega_f = 41.9+2.0957*20 = 83.814 rad/s$

The moment the body reaches the final velocity 0, it will take a period of time and a couple of turns the point at which it stops, then

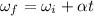
$\omega_f = \omega_i+\alpha t$

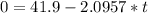
0=41.9-2.0957*t

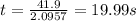
t = (41.9)/(2.0957) = 19.99 s

The angular displacement will then be given by

$\theta = \omega_0*t-(1)/(2)\alpha t$

$\theta=41.9*19.99-0.5*2.0957*19.992$

$\theta= 418.86 rad$

Please log in or register to add a comment.