Question

I need help with this. can somebody help?
​

Answer 1

3x - y + 5 = 0

Explanation:

When two points are given and the equation of the line passing through those points are asked we use two - point form to determine the equation of the line.

Two - point form:
`$ (y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 -x_1) $`

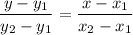
Here the two points are: (2,11) & (-8,-19).

Let
`$ (x_1,y_1) = (2,11) $` and
`$ (x_2, y_2) = (-8,-19) $`

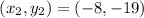
Substituting in the formula we have:

`$ (y - 11)/(-19 - 11) = (x - 2)/(-8 - 2) $`

`$ \implies (y - 11)/(-30) = (x - 2)/(-10) $`

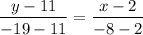
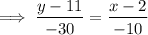
Simplifying we get:

y - 11 = 3x - 6

⇒ 3x - y + 5 = 0