Question

The owner of a computer repair shop has determined that their dailyrevenue has mean $7200 and standard deviation $1200. The dailyrevenue totals for the next 30 days will be monitored. What is the probability that the mean daily revenue for the next 30 days willexceed $7500?

Answer 1

The required probability is 0.0855

Explanation:

Consider the provided information.

The daily revenue has mean $7200 and standard deviation $1200.

`\mu_(\bar x)=7200`

`\sigma=1200`

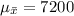
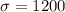
The daily revenue totals for the next 30 days will be monitored.

`\sigma_(\bar x)=(\sigma)/(√(n))`

`\sigma_(\bar x)=(1200)/(√(30))=219.089`

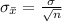
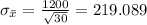
As we know
`Z=(\bar x-\mu_(\bar x))/(\sigma_(\bar x))`

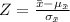
Substitute
`\bar x=7500, \mu_(\bar x)=7200\ and\ \sigma_(\bar x)=219.089` in above formula.

`Z=(7500-7200)/(219.089)=1.3693`

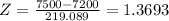
From the standard normal table P( Z >1.3693) = 0.0855

Hence, the required probability is 0.0855