Question

Calculate the force between one grapefruit (mass = 0.322 kg & radius = 0.0685 m) and Earth. Earth has a mass of 6.00E24 kg and a radius of 6.37E6 meters. Assume that the grapefruit is resting on Earth's surface.

a

1.61 N

b

2.10 N

c

2.41 N

d

1.83 N

e

3.18 N

f

3.01 N

g

2.77 N

h

1.97 N

Answer 1

The force acting on the grapefruit present on the surface of earth is 3.18 N.

Answer: Option E

Step-by-step explanation:

It is known that the gravitational force between two masses is directly proportional to the product of the masses and inversely proportional to the square of the distance between them. So, the gravitational force will be

`{\bold \text {Gravitational force}=\frac{G * \text {Product of two } M^(\prime) s}{\left(\text {Distance between the two } M^(\prime) s\right)^(2)}}`

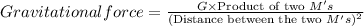
In the present case of determining force acting on a grapefruit due to the gravitational force of Earth, one mass will be mass of the grapefruit and another mass will be mass of the Earth.

The distance between grapefruit and earth is considered as the radius of Earth as it is stated to assume the grapefruit is on the surface of Earth. Let the mass of Earth is denoted as ME and mass of grapefruit be denoted as MG and the distance between them is denoted as r.

`\text{{Gravitational force acting on grapefriut}}=(G * M_(E) * M_(G))/((r)^(2))`

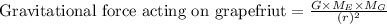
So, by substituting the given values and G value, we get

`\text {Gravitational force acting on grapefriut}=(6.674 * 10^(-11) * 6 * 10^(24) * 0.322)/(\left(6.376 * 10^(6)\right)^(2))`

Hence,

`{\bold \text {{Gravitational force acting on grapefriut}}=(12.8942 * 10^(13))/(40.653 * 10^(12))=0.318 * 10=3.18 N}`

Thus, the force acting on the grapefruit present on the surface of earth is 3.18 N.