Question

A 91.5 kg football player running east at 2.73 m/s tackles a 63.5 kg player running east at 3.09 m/s. what is their velocity afterward? PLEASE HELP

Answer 1

2.88 m/s is the velocity afterward.

Step-by-step explanation:

By using the law of conservation of momentum

Initial momentum = final momentum

`\mathrm{m}_(1) \mathrm{u}_(1)+\mathrm{m}_(2) \mathrm{u}_(2)=\left(\mathrm{m}_(1)+\mathrm{m}_(2)\right) * \mathrm{v} \text { equation }(1)`

`\mathrm{m}_(1)=91.5 \mathrm{kg} \text { is the mass of the first player }\mathrm{m}_(2)=63.5 \mathrm{kg}`

`\mathrm{m}_(2)=63.5 \mathrm{kg} \text { is the mass of the second player }`

`\mathrm{u}_(1)=2.73 \mathrm{m} / \mathrm{s} \text { is the initial velocity of the first player (choosing east as positive direction) }`

`\mathrm{u}_(2)=3.09 \mathrm{m} / \mathrm{s} \text { is the initial velocity of the second player }`

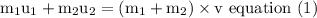
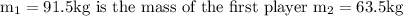
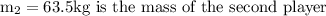
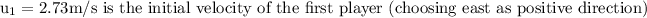
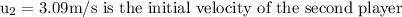
v = is their combined velocity afterwards

Solving equation (1) for v

`V=(m_(1) u_(2)+m_(2) u_(2))/(m_(1)+m_(2))`

`\mathrm{V}=((91.5 * 2.73)+(63.5 * 3.09))/(91.5+63.5)`

`\mathrm{V}=((249.7+196.2))/(155)`

`\mathrm{V}=(445.9)/(155)`

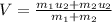
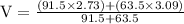
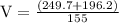
V = 2.88 m/s

Therefore the velocity afterward is 2.88 m/s.