To solve the problem it is necessary to take into account the concepts related to the Magnetic Force, which is given by,
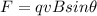
Where
F= Magnetic force
q= charge of proton
v= velocity
B Magnetic field
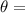 Angle between the velocity and the magnetic field.
Angle between the velocity and the magnetic field.
Re-arrange the equation to find the angle we have,
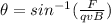
Replacing our values we have,
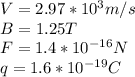
Then,
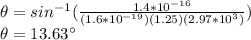
The angle between 0 to 180 degrees would be,
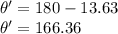
Therefore the two angles required are 13.63° and 166.36°