Question

The human eye can readily detect wavelengths from about 400 nm to 700 nm. If white light illuminates a diffraction grating having 750 lines/mm, over what range of angles does the visible m = 1 spectrum extend?

Answer 1

The range of angles is from 17.50° to 31.76°

Step-by-step explanation:

The diffraction grid equation is as follows:

`dsen\theta=m\lambda`

Clearing for
`\theta`

`sen\theta=(m\lambda)/(d)`

`\theta=sen^(-1)((m\lambda)/(d))`

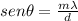
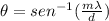
where
`\theta` is the angle,
`m` is the order, in this case
`m=1`,
`\lambda` is the wavelength, and
`d` is defined as follows:

`d=(1)/(resolution)`

and since the resolution is 750 lines/mm wich is the same as
`750lines/1x10^(-3)m`

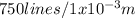
`d` will be:

`d=(1)/(750lines/1x10^(-3)m)=(1x10^(-3)m)/(750lines)=1.33x10^(-6)m`

wich is the distance between each line of the diffraction grating.

substituting the values for
`m` and
`d`:

`\theta=sen^(-1)(((1)\lambda)/((1.33x10^(-6)m)))`

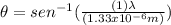
And we need to find two angle values: one for when the wavelength is 400nm and one for when it is 700 nm. So we will get the angle range

`\theta=sen^(-1)(((400x10^(-9)))/((1.33x10^(-6)m)))=17.50`

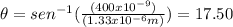
and

`\theta=sen^(-1)(((700x10^(-9)))/((1.33x10^(-6)m)))=31.76`

The range of angles is from 17.50° to 31.76°