Answer:
Rate of change of the area of the rectangle at that instant = 7 cm²/hr.
Explanation:
Area of rectangle = Height x Width
A = hw
The height of a rectangle is increasing at a rate of 3 centimeters per hour and the width of the rectangle is decreasing at a rate of 4 centimeters per hour.

Differentiating area with respect to time,
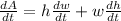
We need to find rate of change of area when the height is 5 centimeters and the width is 9 centimeters.
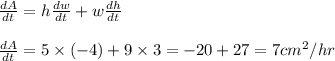
Rate of change of the area of the rectangle at that instant = 7 cm²/hr.