Question

Which statements are true about the ordered pair (−4, 0) and the system of equations? {2x+y=−8x−y=−4 Select each correct answer.

(A) The ordered pair (−4, 0) is a solution to the first equation because it makes the first equation true.
(B) The ordered pair (−4, 0) is a solution to the second equation because it makes the second equation true.
(C) The ordered pair (−4, 0) is not a solution to the system because it makes at least one of the equations false.
(D) The ordered pair (−4, 0) is a solution to the system because it makes both equations true.

Answer 1

(D) The ordered pair (−4, 0) is a solution to the system because it makes both equations true.

Explanation:

Given:

The system of equations are given as:

`2x+y=-8\\x-y=-4`

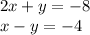
Let us solve this system using elimination method.

Addin the two equations, we get:

`2x+y+x-y=-8-4\\2x+x=-12\\3x=-12\\x=(-12)/(3)=-4`

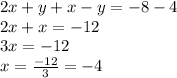
Now, plug in -4 for
`x` in second equation and solve for
`y`.

`x-y=-4\\-4-y=-4\\-y=-4+4\\y=0`

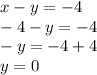
Therefore, the solution to the given system of equations is (-4,0).

This means that the point (-4, 0) satisfies both the equations.

This can be verified as shown below:

Plug in -4 for
`x` and 0 for
`y` and check whether the left side equals right side or not.

`2x+y=-8\\2(-4)+0=-8\\-8+0=-8\\-8=-8\\LHS=RHS\\\\x-y=-4\\-4-0=-4\\-4=-4\\LHS=RHS`

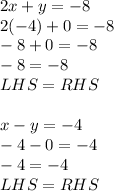
Therefore, the option (D) is correct.