Question

The maker of potato chips uses an automated packaging machine to pack its 20-ounce bag of chips. At the end of every shift 18 bags are selected at random and tested to see if the equipment needs to be readjusted. After one shift, a sample of 18 bags yielded the following data. mean = 20.45 s = .80 n = 18. If we were to conduct a test to see if the sample estimate is different from the company’s expected weight of 20 oz. at an alpha level = .05, what is the conclusion for this test?

Answer 1

Answer with explanation:

Let
`\mu` be the population mean .

By considering the given information in the question , we have

`\text{Null hypothesis }H_0: \mu=20\\\\\text{Alternative hypothesis } H_a: \mu\\eq20`

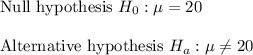
Here,
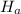`H_a` is two-tailed , so the test is a two-tailed test.

Also, population standard deviation is unknown , so we perform a two-tailed t-test.

For sample size : n= 18

Sample mean :
`\overline{x}=20.45`

Sample standard deviation : s=0.80

Test statistic :

`t=\frac{\overline{x}-\mu}{(s)/(√(n))}`

`t=(20.45-20)/((0.80)/(√(18)))`

`t=(0.45)/((0.80)/(4.2426))`

`t=(0.45)/(0.1885636)`

`t\approx 2.39`

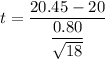
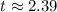
Two-tailed Critical values for
`\alpha=0.05` and degree of freedom df=n-1=17

`t_((\alpha/2,\ df))=t_((0.025,\ 17))=\pm2.11`

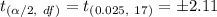
Decision : Since the calculated t-value(2.39) does not lie between the critical values -2.11 and 2.11.

So we reject the null hypothesis .

Conclusion : We have enough evidence at 0.05 significance level to support the claim that the sample estimate is different from the company’s expected weight of 20 oz.