Answer: The cell potential of the cell is +0.03 V
Step-by-step explanation:
The half reactions for the cell is:
Oxidation half reaction (anode):
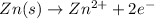
Reduction half reaction (cathode):
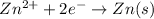
In this case, the cathode and anode both are same. So,
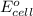 will be equal to zero.
will be equal to zero.
To calculate cell potential of the cell, we use the equation given by Nernst, which is:
![E_(cell)=E^o_(cell)-(0.0592)/(n)\log \frac{[Zn^(2+){diluted}}{[Zn^(2+){concentrated}]}](https://img.qammunity.org/2020/formulas/chemistry/college/939t9ztltglaz3co1hyhmc15ktp17uqy3n.png)
where,
n = number of electrons in oxidation-reduction reaction = 2
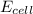 = ?
= ?
![[Zn^(2+){diluted}]](https://img.qammunity.org/2020/formulas/chemistry/college/25i7c49j92bh4jesxeb4yb9kmpgfvr7gg9.png) = 0.010 M
= 0.010 M
![[Zn^(2+){concentrated}]](https://img.qammunity.org/2020/formulas/chemistry/college/sk76usypxker2wd8p850p0ljk2wbbepnip.png) = 0.10 M
= 0.10 M
Putting values in above equation, we get:

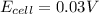
Hence, the cell potential of the cell is +0.03 V