Question

A quantity of 8.10 × 102 mL of 0.600 M HNO3 is mixed with 8.10 × 102 mL of 0.300 M Ba(OH)2 in a constant-pressure calorimeter of negligible heat capacity. The initial temperature of both solutions is the same at 18.46°C. The heat of neutralization when 1.00 mol of HNO3 reacts with 0.500 mol Ba(OH)2 is −56.2 kJ/mol. Assume that the densities and specific heats of the solution are the same as for water (1.00 g/mL and 4.184 J/g · °C, respectively). What is the final temperature of the solution?

Answer 1

22.48°C is the final temperature of the solution.

Step-by-step explanation:

Heat of neutralization of reaction , when 1 mol of nitric acid reacts= ΔH= -56.2 kJ/mol= -56200 J/mol

`Moles (n)=Molarity(M)* Volume (L)`

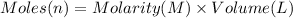
Moles of nitric acid = n

Volume of nitric acid solution =
`8.10* 10^2 mL= 0.81L`

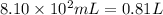
Molarity of the nitric acid = 0.600 M

`n=0.600 M* 0.81 L=0.486 mol`

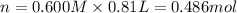
Moles of barium hydroxide = n'

Volume of barium hydroxide solution =
`8.10* 10^2 mL= 0.81L`

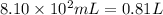
Molarity of the barium hydroxide= 0.300 M

`n'=0.300 M* 0.81 L=0.243 mol`

`2HNO_3+Ba(OH)_2\rightarrow Ba(NO_3)_3+2H_2O`

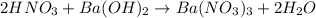
According to reaction, 2 mol of nitric acid reacts with 1 mol of barium hydroxide .Then 0.486 mol of nitric acid will react with :

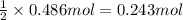`(1)/(2)* 0.486 mol=0.243 mol` barium hydroxide.

Heat release when 0.486 mol of nitric acid reacted = Q

= ΔH × 0.486 = -56200 J/mol × 0.486 mol=-27,313.2 J

Heat absorbed by the mixture after reaction = Q' = -Q = 27,313.2 J

Volume of the nitric solution = 0.81 L = 810 mL

Volume of the ferric nitrate solution = 0.81 L = 810 mL

Total volume of the solution = 810 mL + 810 mL = 1620 mL

Mass of the final solution = m

Density of water = density of the final solution = d = 1 g/mL

`Mass=density* Volume`

`m=1 g/ml* 1620 ml=1620 g`

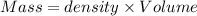
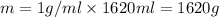
Initial temperature of the both solution were same =
`T_1=18.46^oC`

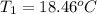
Final temperature of the both solution will also be same after mixing=
`T_2`

Heat capacity of the mixture = c = 4.184 J/g°C

Change in temperature of the mixture = ΔT =
`(T_2-T_1)`

`Q=mc\Delta T=mc(T_2-T_1)`

`27,313.2 J= 1620 g* 4.184 J/g^oC* (T_2-18.46^oC)`

`T_2=22.49^oC`

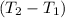
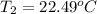
22.48°C is the final temperature of the solution.