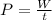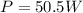Answer:
Part a)
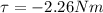
Part b)

Part c)
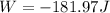
Part d)
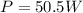
Step-by-step explanation:
Part a)
As we know that torque on the rotating wheel is given as

also we can write this in terms of angular momentum
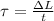
so we have
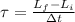
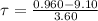
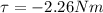
Part b)
Angular displacement of the wheel at constant angular acceleration is given as
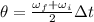
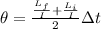
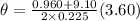

Part c)
Work done on the wheel is equal to the change in kinetic energy of the wheel
so we have
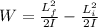
so we have

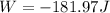
Part d)
Average power is defined as the rate of work done
so it is given as