Question

3. A 2kg wooden block whose initial speed is 3 m/s slides on a smooth floor for 2 meters before it comes to a

stop.
a. Find the coefficient of friction?
b. How much force would be needed to keep the block moving at a constant speed across the floor?

Answer 1

Calculating Coefficient of friction is 0.229.

Force is 4.5 N that keep the block moving at a constant speed.

Step-by-step explanation:

We know that speed expression is as
`\mathrm{V}^(2)=\mathrm{V}_{\mathrm{i}}^(2)+2 . \mathrm{a} . \Delta \mathrm{s}`.

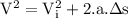Where,
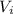`{V}_(i)` is initial speed, V is final speed, ∆s displacement and a acceleration.

Given that,

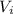`{V}_(i)` =3 m/s, V = 0 m/s, and ∆s = 2 m

Substitute the values in the above formula,

`0=3^(2)-2 * 2 * a`

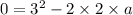
0 = 9 - 4a

4a = 9

`a=2.25 \mathrm{m} / \mathrm{s}^(2)`

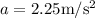
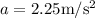`a=2.25 \mathrm{m} / \mathrm{s}^(2)` is the acceleration.

Calculating Coefficient of friction:

`\mathrm{F}=\mathrm{m} * \mathrm{a}`

`\mathrm{F}=\mu * \mathrm{m} * \mathrm{g}`

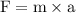
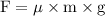
Compare the above equation

`\mu * m * g=m * a`

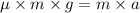
Cancel "m" common term in both L.H.S and R.H.S

`\text { Equation becomes, } \mu * g=a`

`\text { Coefficient of friction } \mu=(a)/(g)`

`\mathrm{g} \text { on earth surface }=9.8 \mathrm{m} / \mathrm{s}^(2)`

`\mu=(2.25)/(9.8)`

`\mu=0.229`

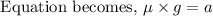
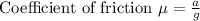
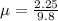
Hence coefficient of friction is 0.229.

calculating force:

`\text { We know that } \mathrm{F}=\mathrm{m} * \mathrm{a}`

`\mathrm{F}=2 * 2.25 \quad(\mathrm{m}=2 \mathrm{kg} \text { given })`

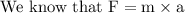
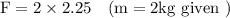
F = 4.5 N

Therefore, the force would be 4.5 N to keep the block moving at a constant speed across the floor.