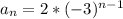Question

The formula for any geometric sequence is an = a1 · rn - 1, where an represents the value of the nth term, a1 represents the value of the first term, r represents the common ratio, and n represents the term number. What is the formula for the sequence 2, -6, 18, -54, ...?

an = 2 · 3 n - 1
an = 2 · (-3) n - 1
an = -3 · 2 n - 1
an = 3 · 2 n - 1

Answer 1

The formula for the sequence is:
`a_n = 2*(-3)^(n-1)`

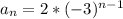
Explanation:

The general term of a geometric sequence is given by:

`a_n = a_1*r^(n-1)`

In which
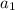`a_1` is the first term and r is the common ratio between the terms, that is, the division between them.

What is the formula for the sequence 2, -6, 18, -54, ...?

First term is 2, so
`a_1 = 2`

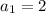
Common ratio is given by:

`r = (-6)/(2) = (18)/(-6) = ... = -3`

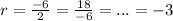
So the sequence is given by:

`a_n = 2*(-3)^(n-1)`