Answer:
(a) The coefficient of friction is 0.153.
(b) Force needed to keep the block moving at a constant speed across the floor is 3 N in the direction opposite to that of frictional force.
Step-by-step explanation:
Given:
Mass of the block is,
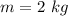
Initial speed of the block is,
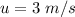
Displacement of the block is,
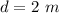
Final speed of the block is,
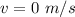
(a)
Using Newton's equations of motion and determining the acceleration of the block:
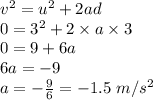
Therefore, frictional force acts on the block to cause the deceleration of the block.
From Newton's second law, net force is product of mass and acceleration.
Here, the only force acting along the motion of the block is friction.
So, friction acting on the block is given as:

Negative sign shows the nature of frictional force that it acts opposite to the motion of the block.
Now, magnitude of frictional force is also given as:
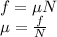
where,
 is the coefficient of friction and
is the coefficient of friction and
 is the normal force.
is the normal force.
Here, there is no vertical motion. So, normal force is equal to weight of the block.
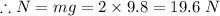
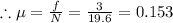
Therefore, the coefficient of friction is 0.153.
(b)
In order to make the speed as constant, the net acceleration acting on the block must be 0. So, the forward force must be equal to the backward frictional force. Hence,
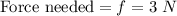
Therefore, force needed to keep the block moving at a constant speed across the floor is 3 N in the direction opposite to that of frictional force.