Question

The table represents the linear function f(x), and the equation represents the linear function g(x). Compare the y-intercepts and slopes of the linear functions f(x) and g(x) and choose the answer that best describes them. x f(x) 0 1 2 9 4 17 g(x) = 3x + 1

Answer 1

The slope of f(x) is greater than the slope of g(x). The y-intercept of f(x) is equal to the y-intercept of g(x). The 3rd option

Step-by-step explanation: this is because i got it right on my test god bless

Answer 2

The y-intercepts of both functions are the same and the function f(x) has a greater slope than the function g(x)

Explanation:

we know that

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

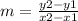
step 1

Determine the slope of the function f(x)

take two points from the table

(0,1) and (2,9)

substitute in the formula

`m=(9-1)/(2-0)`

`m=(8)/(2)`

`m_1=4`

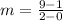
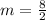
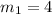
Remember that the y-intercept is the value of y when the value of x is equal to zero

In this problem the point (0,1) is the y-intercept

so

`b_1=1`

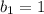
step 2

Determine the slope of the function g(x)

we have

`g(x)=3x+1`

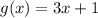
This is the equation of the line in slope intercept form

`y=mx+b`

where

m is the slope

b is the y-intercept

so

In this problem

`m_2=3`

`b_2=1`

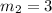
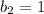
step 3

Compare the y-intercepts and slopes

`b_1=b_2\\m_1 > m_2`

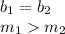
The y-intercepts of both functions are the same and the function f(x) has a greater slope than the function g(x)