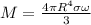Answer:
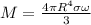
Step-by-step explanation:
As we know that the magnetic moment of a system of rotating charge and its angular momentum is related by an equation given as
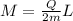
so we can write here angular momentum of the sphere about its diametrical axis as
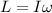
here we have
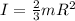
so we have
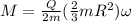
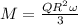
here we know that
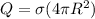
so we have