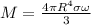Question

A spherical shell of radius R carries a constant surface charge density σ. The shell rotates about its diameter with angular speed ω. Find the magnitude of the magnetic moment of the rotating spherical shell. (Consider the following equation: μ = Q 2m L. Use the following as necessary: π, σ, ω, and R.) μ

Answer 1

`M = (4\pi R^4 \sigma \omega)/(3)`

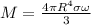
Step-by-step explanation:

As we know that the magnetic moment of a system of rotating charge and its angular momentum is related by an equation given as

`M = (Q)/(2m) L`

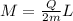
so we can write here angular momentum of the sphere about its diametrical axis as

`L = I\omega`

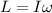
here we have

`I = (2)/(3) mR^2`

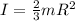
so we have

`M = (Q)/(2m) ((2)/(3) mR^2)\omega`

`M = (QR^2\omega)/(3)`

here we know that

`Q = \sigma (4\pi R^2)`

so we have

`M = (4\pi R^4 \sigma \omega)/(3)`