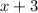Answer:
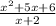
⇒
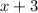
Explanation:
To simplify:
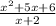
To simplify the given expression we need to factor the numerator.
We have
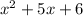
Using split the middle term method by splitting
 into two terms
into two terms
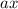 and
and
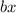 such that
such that
 and
and
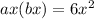
We see that [
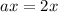 and
and
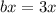 ]
]
Thus we can write
⇒
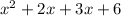
Factoring in pairs by taking the GCF of terms in pairs.
⇒
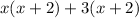
Factoring the whole expression as
 is a common factor.
is a common factor.
⇒
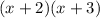
Now, the expression can be rewritten as:
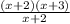
Canceling out the common expressions, we have.
⇒