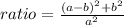Question

What is the ratio of the area of the inner square to the area of the outer

Answer 1

`((a-b)^2+b^2)/(a^(2))`

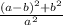
Explanation:

see the attached figure to better understand the problem

we know that

The area of the square is

`A=x^(2)`

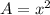
where

x is the length side of the square

step 1

Find the area of the outer square (A_o)

we have that

`x=a\ units`

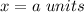
substitute in the formula

`A_o=a^(2)\ units^2`

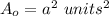
step 2

Find the area of the inner square (A_i)

we know that

The length side of the inner square is equal to the hypotenuse of a right triangle

so

Applying Pythagoras theorem

`x^(2)=(a-b)^2+b^2`

Remember that

`A_i=x^2`

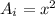
so

`A_i=(a-b)^2+b^2`

step 3

Find the ratio of the area of the inner square to the area of the outer

`ratio=(A_i)/(A_o)`

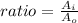
substitute the values

`ratio=((a-b)^2+b^2)/(a^(2))`