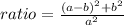Answer:
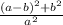
Explanation:
see the attached figure to better understand the problem
we know that
The area of the square is
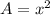
where
x is the length side of the square
step 1
Find the area of the outer square (A_o)
we have that
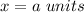
substitute in the formula
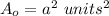
step 2
Find the area of the inner square (A_i)
we know that
The length side of the inner square is equal to the hypotenuse of a right triangle
so
Applying Pythagoras theorem

Remember that
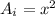
so

step 3
Find the ratio of the area of the inner square to the area of the outer
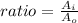
substitute the values