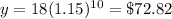Answer:
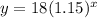
Explanation:
we know that
The equation of a exponential growth function is equal to
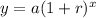
where
y ---> the value of the poster
x ---> the number of years
r ---> is the growth rate of change
a ---> is the initial value
In this problem we have

substitute
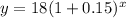
therefore
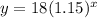
Examples
For x=5 years
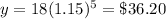
For x=8 years
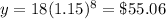
For x=10 years