Question

Monitors manufactured by TSI Electronics have life spans that have a normal distribution with a variance of 2,250,000 and a mean life span of 13,000 hours. If a monitor is selected at random, find the probability that the life span of the monitor will be more than 14,650 hours. Round your answer to four decimal places.

Answer 1

Answer: 0.1357

Explanation:

Given : Monitors manufactured by TSI Electronics have life spans that have a normal distribution with a variance of
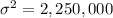`\sigma^2=2,250,000` and a mean life span of
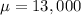`\mu=13,000` hours.

Here ,
`\sigma=√(2250000)=1500`

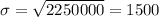
Let x represents the life span of a monitor.

Then , the probability that the life span of the monitor will be more than 14,650 hours will be :-

`P(x>14650)=P((x-\mu)/(\sigma)>(14650-13000)/(1500))\\\\=P(z>1.1)=1-P(z\leq1.1)\ \ [\because\ P(Z>z)=1-P(Z\leq z)]\\\\=1-0.8643339=0.1356661\approx0.1357`

Hence, the probability that the life span of the monitor will be more than 14,650 hours = 0.1357