Answer:
The x -coordinate(s) of the point(s) of intersection of these two polynomials are
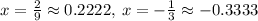
The sum of these x -coordinates is
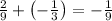
Explanation:
The intersections of the two polynomials, p(x) and q(x), are the roots of the equation p(x) = q(x).
Thus,
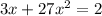 and we solve for x
and we solve for x
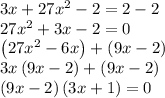
Using Zero Factor Theorem: = 0 if and only if = 0 or = 0
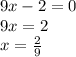
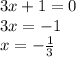
The solutions are:
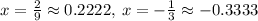
The sum of these x -coordinates is
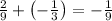
We can check our work with the graph of the two polynomials.