Question

Consider the polynomials p(x) = 3x + 27x^2 and q(x)= 2 . Find the x -coordinate(s) of the point(s) of intersection of these two polynomials. What is the sum of these x -coordinates? (If there is only one point of intersection, give the corresponding x -coordinate.)

Answer 1

The x -coordinate(s) of the point(s) of intersection of these two polynomials are
`x=(2)/(9)\approx0.2222,\:x=-(1)/(3)\approx-0.3333`

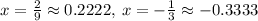
The sum of these x -coordinates is
`(2)/(9)+\left(-(1)/(3)\right)=-(1)/(9)`

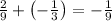
Explanation:

The intersections of the two polynomials, p(x) and q(x), are the roots of the equation p(x) = q(x).

Thus,
`3x + 27x^2=2` and we solve for x

`3x+27x^2-2=2-2\\27x^2+3x-2=0\\\left(27x^2-6x\right)+\left(9x-2\right)\\3x\left(9x-2\right)+\left(9x-2\right)\\\left(9x-2\right)\left(3x+1\right)=0`

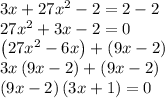
Using Zero Factor Theorem: = 0 if and only if = 0 or = 0

`9x-2=0\\9x=2\\x=(2)/(9)`

`3x+1=0\\3x=-1\\x=-(1)/(3)`

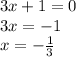
The solutions are:

`x=(2)/(9)\approx0.2222,\:x=-(1)/(3)\approx-0.3333`

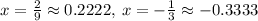
The sum of these x -coordinates is

`(2)/(9)+\left(-(1)/(3)\right)=-(1)/(9)`

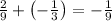
We can check our work with the graph of the two polynomials.