Answer:
The equation of line passing through points (5 , - 4) is 2 x + 5 y + 10 = 0
Explanation:
Given equation of line as
5 x - 2 y = - 6
Now, equation of line in standard form is y = m x + c
where m is the slope
So, 5 x - 2 y = - 6
Or, 2 y = 5 x + 6
Or, y =
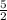 x + 3
x + 3
So, Slope of this line m =
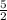
Again , let the slope of other line passing through point (5 , - 4) is M
And Both lines are perpendicular , So , products of line = - 1
i.e m × M = - 1
Or, M = -

Or, M = -
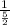 = -
= -

So, equation of line with slope M and points (5, - 4) is
y -
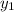 = M × (x -
= M × (x -
 )
)
Or, y - ( - 4 ) = -
 × ( x - 5 )
× ( x - 5 )
Or, y + 4 = -
 x +
x +
 × 5
× 5
Or, y + 4 = -
 x + 2
x + 2
or, y + 4 - 2 = -
 x
x
or, y + 2 = -
 x
x
Or, 5×(y + 2) = - 2 x
∴ 5 y + 10 = - 2 x
I.e 2 x + 5 y + 10 = 0
Hence The equation of line passing through points (5 , - 4) is 2 x + 5 y + 10 = 0 Answer