Question

The height (in inches) of men at UH is assumed to have a normal distribution with a standard deviation of 3.6 inches. The height (in inches) of women at UH is also assumed to have a normal distribution with a standard deviation of 2.9 inches. A random sample of 49 men and 38 women yielded respective means of 68.3 inches and 64.6 inches. Find the 90% confidence interval for the difference in the heights of men at UH and women at UH

Answer 1

Answer: The required 90% confidence interval would be (2.55,4.85).

Explanation:

Since we have given that

Standard deviation of men = 3.6 inches

Standard deviation of women = 2.9 inches

Average of men = 68.3 inches

Average of women = 64.6 inches

Number of men = 49

Number of women = 38

α = 0.10

`(\alpha )/(2)=(0.10)/(2)=0.05\\\\So,\\\\z_(0.05)=1.645`

So, the confidence interval would be

`(\bar{x_1}}-\bar{x_2}})\pm z\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}\\\\=(68.3-64.6)\pm 1.645\sqrt{(3.6^2)/(49)+(2.9^2)/(38)}\\\\=3.7\pm 1.645* 0.69\\\\=(3.7-1.15,3.7+1.15)\\\\=(2.55,4.85)`

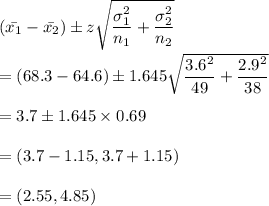
Hence, the required 90% confidence interval would be (2.55,4.85).