Question

What are the coordinates of the vertex of the parabola represent by the equation y=-5x^2+30x-25

Answer 1

The coordinate of the vertex of the parabola is (h,k) = (3,20)

Explanation:

The given equation of the parabola is
`y=-5x^2+30x-25`

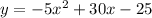
Now, the General Parabolic Equation is of the form:

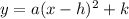`y = a (x-h)^2 + k`, then the vertex is the point (h, k).

Now, to covert the given equation in the standard form:

`y=-5x^2+30x-25   = -5(x^2  -6x   + 5)`

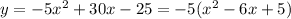
Using the COMPLETE THE SQUARE METHOD,

`-5(x^2  -6x   + 5)  = -5(x^2  -6x  +  (3)^2 +  5  - (3)^2)\\\implies -5(((x^2  -6x +(3)^2)  + 5 - 9)\\= -5((x-3)^3 -4)\\= -5(x-3)^2 + 20`

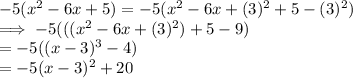
or
`y = -5(x-3)^2 + 20`

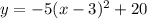
⇒The general formed equation of the given parabola is

`y  = -5(x-3)^2 + 20`

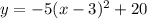
Comparing this with general form, we get

h = 3, k = 20

Hence, the coordinate of the vertex of the parabola is (h,k) = (3,20)