Answer:
The arch above the road is 251 meters from the left pylons
Explanation:
we have
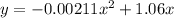
This is a vertical parabola open downward (because the leading coefficient is negative)
The vertex is a maximum
The y-coordinate of the vertex represent the maximum height of the arch above the road
Remember that the x-coordinate of the vertex is the midpoint between the roots of the quadratic equation
One root is the origin (0,0)
Determine the second root
For y=0
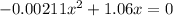
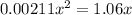
Simplify
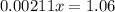

Find the midpoint between the roots
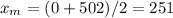
so
The x-coordinate of the vertex is 251
therefore
The arch above the road is 251 meters from the left pylons
see the attached figure to better understand the problem