Question

Scientists discover two planets orbiting a distant star. The average distance from the star to Planet A is 4 AU, and it takes 432 Earth days for Planet A to orbit the star. If it takes 1,460 days for Planet B to complete an orbit, what is the average distance from Planet B to the star?

A. 6 AU
B. 8 AU
C. 9 AU
D. 13.5 AU

Answer 1

C. 9 AU

Explanation:

The period (T) of Planet A is 432365=1.2 Earth years. The period of Planet B is 1,458365=4.0 Earth years. Kepler's Third Law states that

a3=kT2

Substituting the known values of a and T for Planet A, we have

43=k⋅1.22

64=k⋅1.4

k=45.7

Using this value for k, we can solve for the distance from Planet B to the star

a3=45.7⋅4.02

a3=731.2

a=9.0AU

An alternative solution is to notice that a3T2=k for both orbits, which means that the ratio a3T2 is the same for both orbits. So, 434322=x314582. Solving this proportion gives x3=729, so x=9.0AU.

Answer 2

Option C - 9 AU

Explanation:

To find : What is the average distance from Planet B to the star?

Solution :

According to kepler's law,

The squares of the sidereal periods (of revolution) of the planets are directly proportional to the cubes of their mean distances from the Sun.

i.e.
`P^2\propto S^3`

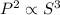
We have given,

The average distance from the star to Planet A is
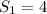`S_1=4` AU.

It takes 432 Earth days for Planet A to orbit the star i.e.
`P_1=432`

It takes 1,460 days for Planet B to complete an orbit i.e.
`P_2=1460`

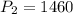
Substitute the values in
`((P_1)/(P_2))^2=((S_1)/(S_2))^3`

`((432)/(1460))^2=((4)/(S_2))^3`

`0.0875=((4)/(S_2))^3`

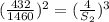
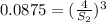
Taking root cube both side,

`\sqrt[3]{0.0875}=(4)/(S_2)`

`0.444=(4)/(S_2)`

`S_2=(4)/(0.444)`

`S_2=9.00`

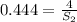
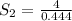
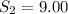
The average distance from Planet B to the star is 9 AU.

Therefore, Option C is correct.