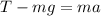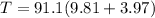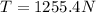Question

The drawing shows Robin Hood (mass = 91.1 kg) about to escape from a dangerous situation. With one hand, he is gripping the rope that holds up a chandelier (mass = 215.0 kg). When he cuts the rope where it is tied to the floor, the chandelier will fall, and he will be pulled up toward a balcony above. Ignore the friction between the rope and the beams over which it slides, and find (a) the acceleration with which Robin is pulled upward and (b) the tension in the rope while Robin escapes.

Answer 1

Part a)

`a = 3.97 m/s^2`

Part b)

`T = 1255.4 N`

Step-by-step explanation:

Part a)

By force equation at position of Robinhood we will have

`T - mg = ma`

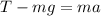
on the other side of the rope we will have

`Mg - T = Ma`

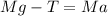
now by above two equations we have

`Mg - mg = (M + m) a`

`a = (M - m)/(M + m) g`

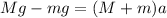
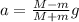
plug in all data in the equation we will have

`a = (215 - 91.1)/(215 + 91.1)(9.81)`

`a = 3.97 m/s^2`

Part b)

From above equation we have

`T - mg = ma`

`T = mg + ma`

`T = 91.1(9.81 + 3.97)`

`T = 1255.4 N`