Question

Trigonometry - Verify Identity:

cos (x - y) / sin (x + y) = 1 + cotxcoty / cotx + coty

Answer 1

The proof is given below.

Explanation:

Given:

The identity to verify is given as:

`(\cos (x-y))/(\sin (x+y))=(1+\cot x.\cot y)/(\cot x+\ cot y)`

Consider the left hand side of the identity.

`\because \cos (A-B)=\cos A\cdot \cos B+\sin A\cdot \sin B\\ \sin (A+B)=\sin A\cdot \cos B+\sin B\cdot \cos A`

`= (\cos (x-y))/(\sin (x+y))\\=(\cos x\cdot \cos y+\sin x\cdot \sin y)/(\sin x\cdot \cos y+\sin y\cdot \cos x)\\`

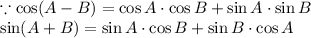
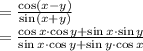
Dividing both numerator and denominator by
`\sin x\cdot \sin y`. This gives,

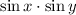`=((\cos x\cdot \cos y)/(\sin x\cdot \sin y)+(\sin x\cdot \sin y)/(\sin x\cdot \sin y))/((\sin x\cdot \cos y)/(\sin x\cdot \sin y)+(\sin y\cdot \cos x)/(\sin x\cdot \sin y)) \\\\\\=(\cot x\cdot \cot y+1)/(\cot x+\cot y)\\\\=(1+\cot x.\cot y)/(\cot x+\ cot y)=RHS`

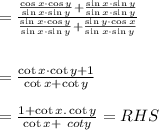
We have used the identity
`\cot A = (\cos A)/(\sin A)` above.

Therefore,

`(\cos (x-y))/(\sin (x+y))=(1+\cot x.\cot y)/(\cot x+\ cot y)`

Therefore, LHS = RHS and hence proved.