Question

High-pressure liquid chromatography (HPLC) is a method used in chemistry and biochemistry to purify chemical substances. The pressures used in this procedure range from around 500 kilopascals (500,000 Pa) to about 60,000 kPa (60,000,000 Pa). It is often convenient to know the pressure in torr. If an HPLC procedure is running at a pressure of 2.04×108 Pa , what is its running pressure in torr?

B)A sample of gas in a balloon has an initial temperature of 37 ∘C and a volume of 1.12×103 L . If the temperature changes to 58 ∘C , and there is no change of pressure or amount of gas, what is the new volume, V2, of the gas?

C)A very flexible helium-filled balloon is released from the ground into the air at 20. ∘C. The initial volume of the balloon is 5.00 L, and the pressure is 760. mmHg. The balloon ascends to an altitude of 20 km, where the pressure is 76.0 mmHg and the temperature is −50. ∘C. What is the new volume, V2, of the balloon in liters, assuming it doesn't break or leak?

D )Consider 4.60 L of a gas at 365 mmHg and 20. ∘C . If the container is compressed to 2.40 L and the temperature is increased to 30. ∘C , what is the new pressure, P2, inside the container? Assume no change in the amount of gas inside the cylinder.

Answer 1

Step-by-step explanation:

A) Pressure at which HPLC procedure is running = P =
`2.04* 10^8 Pa`

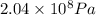
1 Torr = 133.322 Pascal

`P=2.04* 10^8 Pa=(2.04* 10^8 )/(133.322 ) Torr=1,530.13 Torr`

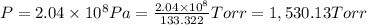
The running pressure in Torr is 1,530.13.

B)Initial temperature if the gas in balloon =
`T_1=37^oC=310.15 K`

Initial volume of the gas in the balloon =
`V_1=1.12* 10^3 L`

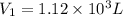
Final temperature if the gas in balloon =
`T_2=58^oC=331.15 K`

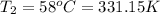
Final volume of the gas in the balloon =
`V_2=?`

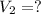
Using Charles law:

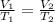`(V_1)/(T_1)=(V_2)/(T_2)` (constant pressure)

`V_2=(V_1* T_2)/(T_1)=(1.12* 10^3 L* 331.15 K)/(310.15 K)=1.196* 10^3 L`

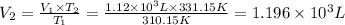
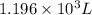`1.196* 10^3 L` is the new volume of the gas.

C) Initial temperature if the gas in balloon =
`T_1=20^oC=293.15 K`

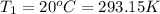
Initial volume of the gas in the balloon =
`V_1=5.00 L`

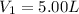
Initial pressure of the gas in the balloon =
`P_1=760 mmHg`

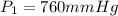
Final temperature if the gas in balloon =
`T_2=-50^oC=223.15 K`

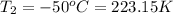
Final volume of the gas in the balloon =
`V_2=?`

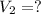
Final pressure of the gas in the balloon =
`P_2=76 mmHg`

Using combine gas law:

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

`V_2=(P_1V_1* T_2)/(T_1* P_2)`

`=(760 mmHg* 5.00 L* 23.15 K)/(293.15 K* 76 mmHg)`

`V_2=38.06 L`

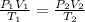
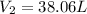
38.06 liters is the new volume of the balloon.

D) Initial temperature if the gas in container=
`T_1=20^oC=293.15 K`

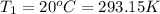
Initial volume of the gas in the container =
`V_1=4.60 L`

Initial pressure of the gas in the container=
`P_1=365 mmHg`

Final temperature if the gas in container=
`T_2=30^oC=303.15 K`

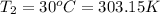
Final volume of the gas in the container=
`V_2=2.40 L`

Final pressure of the gas in the container=
`P_2=?`

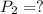
Using combine gas law:

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

`P_2=(P_1V_1* T_2)/(T_1* V_2)`

`=(365 mmHg* 4.60 L* 303.15 K)/(293.15 K* 2.4 L)`

`P_2=723.45 mmHg`

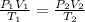
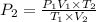
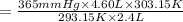
723.45 mmHg is the new pressure inside the container.