Question

Suppose 1.26 g of C2(NO2)6(s) is placed in a 200.0 cm3 vessel where it is detonated.

The heat capacities, Cv, at 25 °C for the gases formed are as follows:
CO2: 28.5 J mol-1 K-1
NO: 21.5 J mol-1 K-1
NO2: 29.5 J mol-1 K-1
Assuming the heat capacities don’t change and all the heat liberated in the reaction remains in the container, what will be the pressure of the mixture of gases after detonation?

Answer 1

Step-by-step explanation:

It is given that 1.26 g of
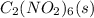`C_(2)(NO_(2))_(6)(s)` is placed in a
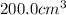`200.0 cm^(3)` vessel.

The balanced equation for the given reaction will be as follows.

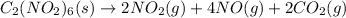`C_(2)(NO_(2))_(6)(s) \rightarrow 2NO_(2)(g) + 4NO(g) + 2CO_(2)(g)`, \Delta H_{rxn}[/tex] = -455.66 kJ

Now,
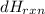`dH_(rxn)` for 1.26g
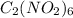`C_(2)(NO_(2))_(6)` will be as follows.

`dH_(rxn) = 1.26g C_(2)(NO_2)_6 * ((1 mol C_2(NO_2)_6)/(300.08g) C_2(NO_2)_6) * -451.1 kJ/mol C_2(NO_2)_6)`

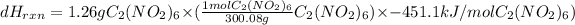
= -1.895 kJ

Now, we will calculate the moles of
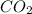`CO_2`, NO and [/tex]NO_2[/tex] formed as follows.

• Moles of
  `NO_(2) = 1.26g C_2(NO_2)_6 * ((1 mol C_2(NO_2)_6)/(300.08g C_2(NO_2)_6)) * ((2 mol NO_(2))/(1 mol C_2(NO_2)_6))`

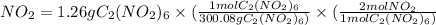
= 0.008398 mol
`NO_2`

• Moles of NO =
  `1.26 g C_2(NO_2)_6 * ((1 mol C_2(NO_2)_6)/(300.08 g C_2(NO_2)_6)) * ((4 mol NO)/(1 mol C_2(NO_2)_6))`

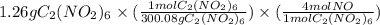
= 0.01680 mol NO

• Moles
  `CO_(2) = 1.26 g C_2(NO_2)_6 * ((1 mol C_2(NO_2)_6)/( 300.08 g C_2(NO_2)_6)) * ((2 mol CO_2)/(1 mol C_2(NO_2)_6))`

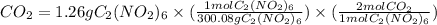
= 0.008398 mol
`CO_2`

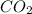
According to energy balance, we assume the same final temperature, assuming we heat the mix to
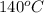`140^(o)C` to make the reaction occur.

Then, calculate heat as follows.

Heat =
`(m * C_v * (T_(f) - 140^(o)C) CO_(2) + (m * C_(v) * (T_(f) - 140^(o)C) NO + (m * C_(v) * (T_(f) - 140^(o)C) NO_2`

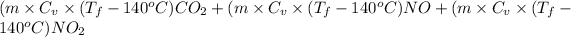
1895 J =
`(0.008398 mol NO_2 * 29.5 J/mol^(o)C * (T_(f) - 140^(o)C)) + (0.01680 mol NO * 21.5 J/mol^(o)C * (T_(f) - 140^(o)C)) + (0.008398 mol CO_(2) * 28.5 J/mol^(o)C * (T_(f) - 140^(o)C))`

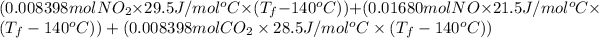
1895 =
`0.2477 * (T_(f) - 140) + 0.3611 * (T_(f) - 140) + 0.2393 * (T_(f) - 140)`

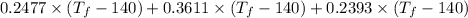
On rearranging the above equation we will calculate the final temperature as follows.

`T_(f) = ((1895)/((0.2477 + 0.3611 + 0.2393))) + 140`

=
`2374^(o)C`

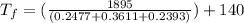
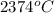
= 2647 K

According to the ideal gas equation, PV = nRT.

So, calculate the pressure as follows.

P =
`(nRT)/(V)`

=
`(0.008398 + 0.01680 + 0.008398) * (0.08206 L atm/mol K) * \frac {2647 K}{0.2000 L}`

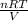
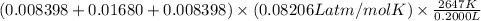
= 36.5 atm

Thus, we can conclude that the pressure of the mixture of gases after detonation is 36.5 atm.