Answer:
92.25m
Step-by-step explanation:
In order to solve the exercise, it is necessary to apply the concept of construtive interference due to a path difference.
The formula is given by,
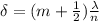
where,
n is the index of refraction of the medium in which the wave is traveling
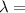 wavelenght
wavelenght
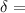 is the path difference
is the path difference
m = integer (0,1,2,3...)
Since in this case we are dealing with an atmospheric environment, where air is predominant, we approximate n to 1.
And since we need the reflected wave,
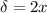
Where x is the distance in one direction without return.
The distance must correspond to the minimum therefore m = 0, so
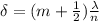
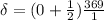
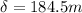
Then the minimum distance is:
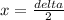
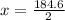
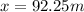
Therefore the minimum distance from the mountain to the receiver that produces destructive interference at the receiver is 92.25m