Question

If the population of a town is decreasing by 4% per year and started with 12,500 residents, which of the following is its projected population in 10 years?

1-9,230
2-76
3-18,503
4-8,310

Answer 1

The population after 10 years will be 8310 approximately.

Option - 4

SOLUTION:

Given that, the population of a town is decreasing by
`4\%` per year and started with 12,500 residents,

We have to find its projected population in 10 years. We can use the formula

`\text { present population }=\text { previous population } *\left(1-\frac{\text {rate}}{100}\right)^{\text {times* period }}`

Then, population after 10 years
`=12500 *\left(1-(4)/(100)\right)^(10)`

`\begin{array}{l}{\Rightarrow 12500 *(1-0.04)^(10)} \\\\ {\Rightarrow 12500 * 0.96^(10)} \\\\ {\Rightarrow 12500 * 0.6648} \\\\ {\Rightarrow 8310.407\rightarrow 8310.407\approx 8310}\end{array}`

ROUNDING OFF RULES:

Step 1: First, look at the digit to the immediate right of rounding off the digit

Step 2: If that digit is less than 5, do not change the rounding digit but drop all digits to the right of it.

Step 3: If that digit is greater than or equal to five, add one to the rounding digit and drop all digits to the right of it.

Answer 2

The population of town after 10 years is 8300 unit .

Explanation:

Given as :

The rate of decrease of population of town = 4%

The initial population of town = 12,500 unit

Let The population of town after 10 years = P

So ,

The population of town after n years = initial population ×
`(1-(Rate)/(100))^(n)`

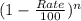
Or, The population of town after 10 years = 12,500 ×
`(1-(4)/(100))^(10)`

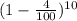
Or, The population of town after 10 years = 12,500 ×
`(0.96)^(10)`

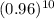
∴ The population of town after 10 years = 12,500 × 0.664 = 8300 unit

Hence The population of town after 10 years is 8300 unit . Answer